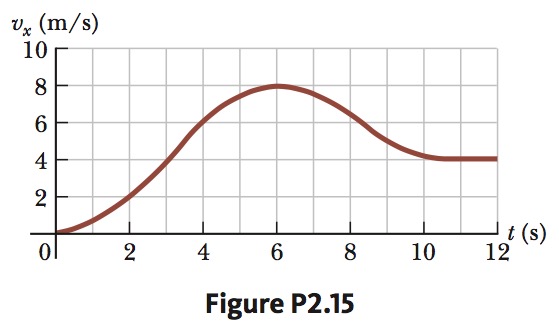
2. Figure P2.15 shows a graph of `v_x` versus `t` for the motion of a motorcyclist as he starts from rest and moves along the road in a straight line.
(a) Find the average acceleration for the time interval `t = 0` to `t = 6.00 s`.
(b) Estimate the time at which the acceleration has its greatest positive value and the value of the acceleration at that instant.
(c) When is the acceleration zero?
(d) Estimate the maximum negative value of the acceleration and the time at which it occurs.
Hint
The slop of the curve is the acceleration
Answer
(a) `a =1.3 m//s^2`
(b) `a =2 m//s^2` at `t = 3s`
(c) `a = 0` at `t=6s` and `t > 10s`
(d) `a=1.5 m//s^2` at ` t=8 s`
Show Steps
(a)
Read From graph:
when `t=0s` `v(0)=0`
when `t=6s` `v(6)=8 m//s`
Average acceleration:
`overline(a) = (v(6)-v(0))/(∆t)`
`overline(a) = (8 m//s-0)/(6s -0) = color(red)(1.3 m//s^2)`
(b)
We know that, the instantaneous acceleration is the slop of the curve. As we can see from this graph, the cure has the maximum positive slope at around `t=3`.
From this graph we assume this slop at `t=3` equals the slop from `t=2` to `t=4`
when `t=2s` `v(2)=2 m//s`
when `t=4s` `v(4)=6 m//s`
acceleration:
`a = (v(4)-v(2))/(∆t)`
`a = (6 m//s-2 m//s)/(4s -2s) = color(red)(2 m//s^2)`
(c)
The acceleration is 0 when the slop at that point is 0
Form the graph we know the slop at `t = 6s` and `t>10` is 0,
`a = 0` when `color(red)(t=6s)` and `color(red)(t>10s)`
(d)
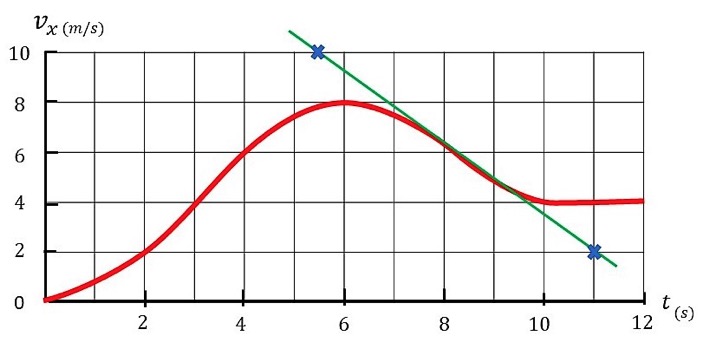
Maximum negative acceleration occurs when above graph has its maximum negative slop , at `color(red)(t=8s)`
if we add a tangent line (the green line in above graph) at `t=8s`
we get :
when `t=7s` `v(7)=8 m//s`
when `t=9s` `v(9)=5 m//s`
acceleration:
`a = (v(9)-v(7))/(∆t)`
`a = (5 m//s-8 m//s)/(9s -7s) = color(red)(-1.5 m//s^2)`
|


