|
2. A proton, which is the nucleus of a hydrogen atom, can be modeled as a sphere with a diameter of `2.4 fm` and a mass of `1.67 \times 10^(-27) kg`.
(a)Determine the density of the proton.
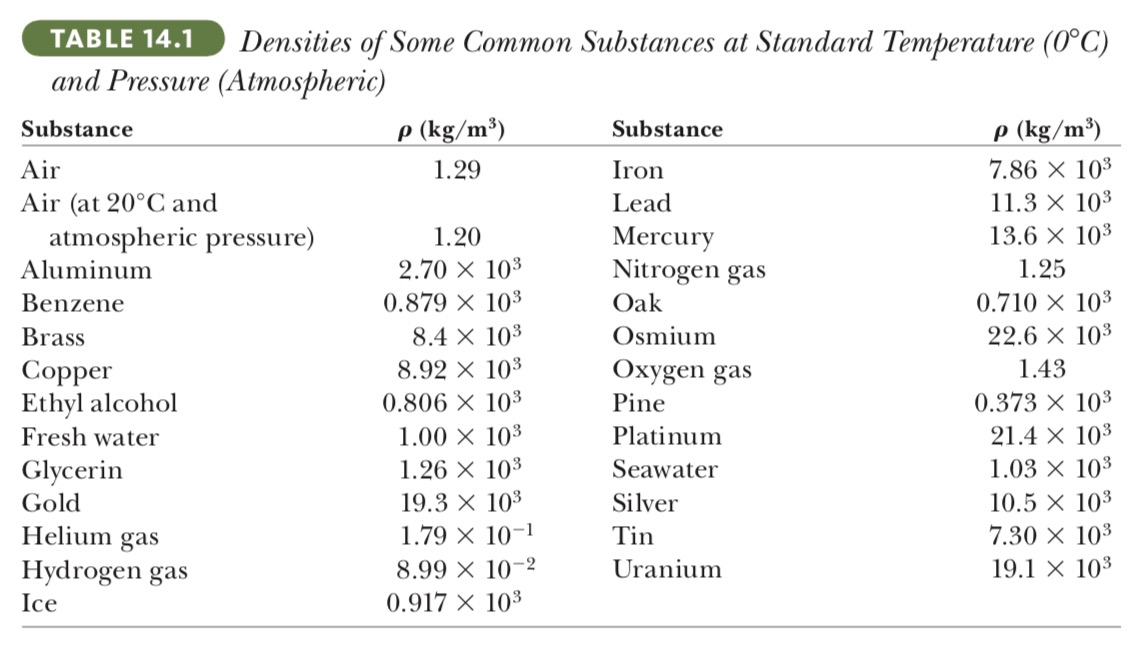
(b) State how your answer to part (a) compares with the density of osmium, given in Table 14.1
 `1fm = 10^(-15) m`, `ρ=m/V`, `V=4/3πr^3`
(a) `ρ_p = 2.3 times 10^(17) kg//m^3`
(b) The density of a proton is `1.02 times 10^(13) ` times of the density of osmium.
Knowns:
Diameter of proton: `d_p=2.4fm => r_p = 1.2fm = 1.2 times 10(-15) m`
Mass of proton: `m_p = 1.67 times 10^(-27) kg`
(a)
Density of proton:
`ρ_p = m_p /V_p = m_p/(4/3πr_p^3)`
`ρ_p = (1.67 times 10^(_27) kg) /(4/3π(1.2 times 10^(-15))^3)`
`ρ_p = 2.3times 10^(17) kg//m^3`
(b)
Let's pick osmium as a sample in table 14.1
`ρ_(os) = 22.6 times 10^3 kg//m^3`
`ρ_p/ρ_(os) = (2.3times10^(17) kg//m^3)/(22.6 times 10^3 kg//m^3) = 1.02 times 10^(13)`
So the density of a proton is `1.02 times 10^(13) ` times of the density of osmium.
|
