|
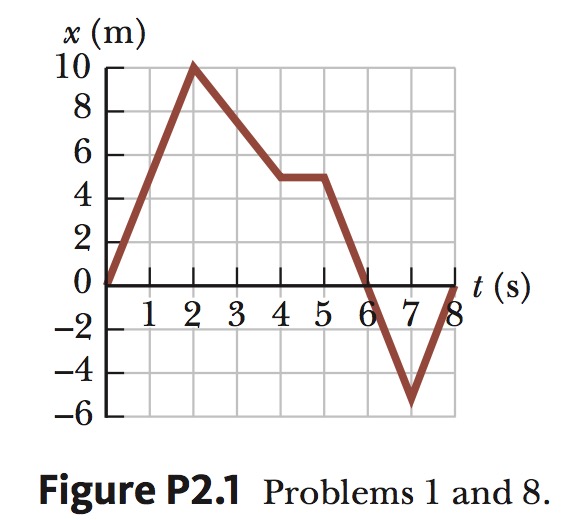
1. The position versus time for a certain particle moving along the x axis is shown in Figure P2.1. Find the average velocity in the time intervals
(a) 0 to 2s,
(b) 0 to 4s,
(c) 2s to 4s,
(d) 4s to 7s,
(e) 0 to 8s.
 average velocity: `V_a = (∆x)/(∆t)`
(a) `5.0 m//s`
(a) `1.3 m//s`
(a) `-2.5 m//s`
(a) `-3.3 m//s`
(a) `0 m//s`
Known: `V_a = (∆x)/(∆t)`
(a) `x`: `0m to 10m` and `t`: `0s to 2s`
`V_a = (10m-0m)/(2s-0s) = 5.0 m//s `
(b) `x`: `0m to 5m` and `t`: `0s to 4s`
`V_a = (5m-0m)/(4s-0s) = 1.3 m//s `
(c) `x`: `10m to 5m` and `t`: `2s to 4s`
`V_a = (5m-10m)/(4s-2s) = -2.5 m//s `
(d) `x`: `5m to -5m` and `t`: `4s to 7s`
`V_a = (-5m-5m)/(7s-4s) = -3.3 m//s `
(a) `x`: `0m to 0m` and `t`: `0s to 8s`
`V_a = (0m-0m)/(8s-0s) = 0 m//s `
|
