dimensional analysis
The method of dimensional analysis is very powerful in solving physics problems. Dimensions can be treated as algebraic quantities. By making estimates and performing order-of-magnitude calculations, you should be able to approximate the answer to a problem when there is not enough information available to specify an exact solution completely.
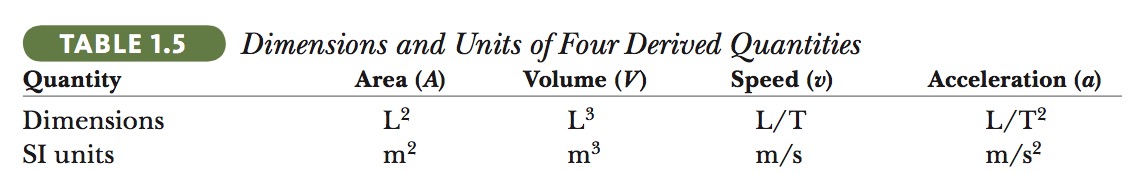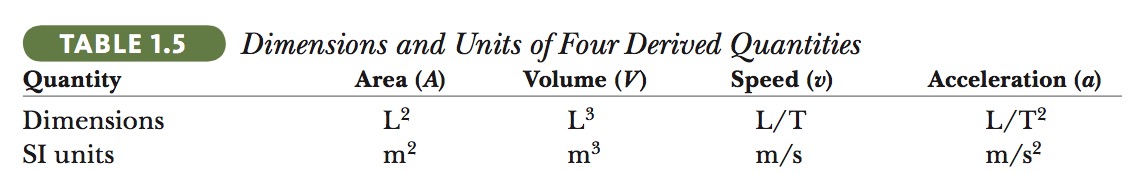In many situations, you may have to check a specific equation to see if it matches your expectations. Dimensional analysis can be used because dimensions can be treated as algebraic quantities.
Example:
`x = 1/2at^2`
dimensional analysis:
`x=>L`
`1/2` is a constant without a unit
`a => L/T^2`
`t => T`
The dimensional form of the equation is:
`L = L/T^2 T^2 = L`
In many situations, you may have to check a specific equation to see if it matches your expectations. Dimensional analysis can be used because dimensions can be treated as algebraic quantities.
Example:
`x = 1/2at^2`
dimensional analysis:
`x=>L`
`1/2` is a constant without a unit
`a => L/T^2`
`t => T`
The dimensional form of the equation is:
`L = L/T^2 T^2 = L`