Freely Falling Objects
• free-fall acceleration: `g`
• magnitude of `g`: `9.80\ m//s^2`
• direction of acceleration: downward or (`a_y = -g=-9.80\ m//s^2`)
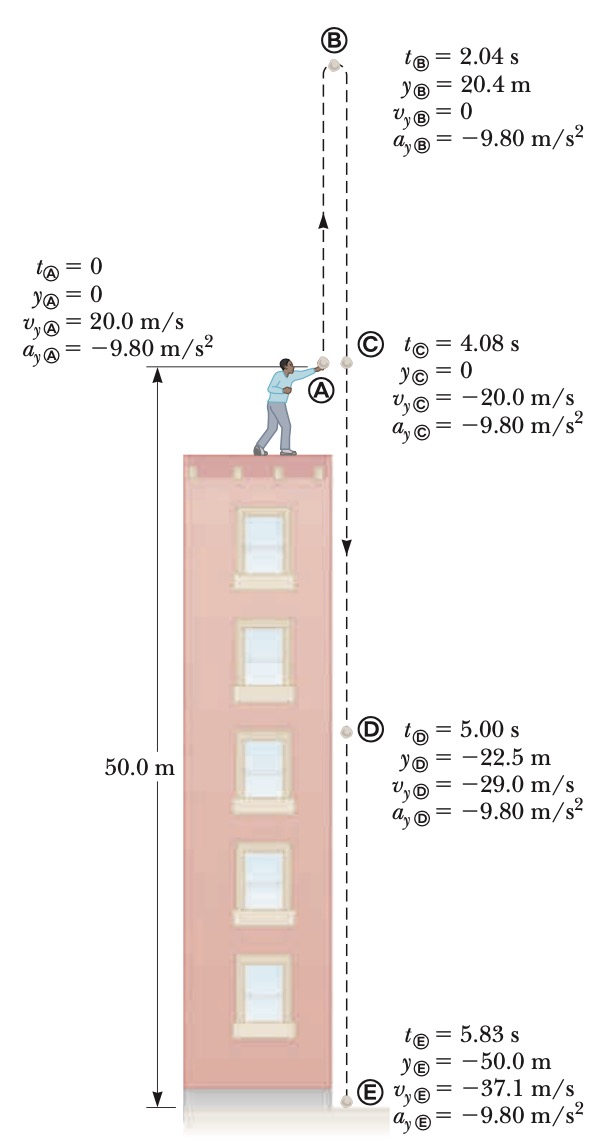 (A) Using `t_A= 0` as the time the stone leaves the thrower’s hand at position `A`, determine the time at which the stone reaches its maximum height.
Given:
`v_i = 20.0\ m//s`
`g = -9.80\ m//s`
`v_f = 0`
Use Equation: `v_f = v_i + g t`
`=> t = (v_f - v_i)/g`
`=>t=(0-20.0)/9.80 = 20.4 s`
(B) Find the maximum height of the stone.
set `y_i = y_A=0`
`y_f = y_(max) = y_B`
`y_B = y_A +v_it + 1/2 g t^2`
`y_B = 0 + (20.0\ m//s)(2.04\ s) + 1/2(-9.80\ m//s^2)(2.04\ s)^2`
`y_B = 20.4\ m`
(C) Determine the velocity of the stone when it returns to the height from which it was thrown.
Know:`Y_A = Y_C =0`
`v_C^2 = V_A^2 + 2a(Y_C-Y_A)`
Know:`Y_A = Y_C =0`
`=>v_C^2 = V_A^2`
`=> v_C = ±V_A`
since V_C and V_A are opposite,
`=> V_C = - V_A = -20.0\ m//s`
(D) Find the velocity and position of the stone at `t = 5.00\ s`.
`v_D = v_i + g t`
`= 20.0\ m//s + (-9.80\ m//s^2)(5.00\ s)`
`=-29.0\ m//s`
`y_D = y_i + v_it + 1/2g t^2`
`= 0 + (20.0\ m//s)(5.00\ s) +1/2(-9.80\ m//s^2)(5.00\ s)`
`=-22.5 m`
(A) Using `t_A= 0` as the time the stone leaves the thrower’s hand at position `A`, determine the time at which the stone reaches its maximum height.
Given:
`v_i = 20.0\ m//s`
`g = -9.80\ m//s`
`v_f = 0`
Use Equation: `v_f = v_i + g t`
`=> t = (v_f - v_i)/g`
`=>t=(0-20.0)/9.80 = 20.4 s`
(B) Find the maximum height of the stone.
set `y_i = y_A=0`
`y_f = y_(max) = y_B`
`y_B = y_A +v_it + 1/2 g t^2`
`y_B = 0 + (20.0\ m//s)(2.04\ s) + 1/2(-9.80\ m//s^2)(2.04\ s)^2`
`y_B = 20.4\ m`
(C) Determine the velocity of the stone when it returns to the height from which it was thrown.
Know:`Y_A = Y_C =0`
`v_C^2 = V_A^2 + 2a(Y_C-Y_A)`
Know:`Y_A = Y_C =0`
`=>v_C^2 = V_A^2`
`=> v_C = ±V_A`
since V_C and V_A are opposite,
`=> V_C = - V_A = -20.0\ m//s`
(D) Find the velocity and position of the stone at `t = 5.00\ s`.
`v_D = v_i + g t`
`= 20.0\ m//s + (-9.80\ m//s^2)(5.00\ s)`
`=-29.0\ m//s`
`y_D = y_i + v_it + 1/2g t^2`
`= 0 + (20.0\ m//s)(5.00\ s) +1/2(-9.80\ m//s^2)(5.00\ s)`
`=-22.5 m`
`v_f = v_i + g t`
`v_(avg) = (v_i + v_f)/2`
`y_f = y_i + 1/2(v_i + v_f)t`
`y_f = y_i + v_it + 1/2 g t^2`
`v_f^2 = v_i^2 + 2g(y_f - y_i)`
Example:
A stone thrown from the top of a building is given an initial velocity of `20.0\ m//s` straight upward. The stone is launched `50.0\ m` above the ground, and the stone just misses the edge of the roof on its way down as shown in the Figure.
 (A) Using `t_A= 0` as the time the stone leaves the thrower’s hand at position `A`, determine the time at which the stone reaches its maximum height.
Given:
`v_i = 20.0\ m//s`
`g = -9.80\ m//s`
`v_f = 0`
Use Equation: `v_f = v_i + g t`
`=> t = (v_f - v_i)/g`
`=>t=(0-20.0)/9.80 = 20.4 s`
(B) Find the maximum height of the stone.
set `y_i = y_A=0`
`y_f = y_(max) = y_B`
`y_B = y_A +v_it + 1/2 g t^2`
`y_B = 0 + (20.0\ m//s)(2.04\ s) + 1/2(-9.80\ m//s^2)(2.04\ s)^2`
`y_B = 20.4\ m`
(C) Determine the velocity of the stone when it returns to the height from which it was thrown.
Know:`Y_A = Y_C =0`
`v_C^2 = V_A^2 + 2a(Y_C-Y_A)`
Know:`Y_A = Y_C =0`
`=>v_C^2 = V_A^2`
`=> v_C = ±V_A`
since V_C and V_A are opposite,
`=> V_C = - V_A = -20.0\ m//s`
(D) Find the velocity and position of the stone at `t = 5.00\ s`.
`v_D = v_i + g t`
`= 20.0\ m//s + (-9.80\ m//s^2)(5.00\ s)`
`=-29.0\ m//s`
`y_D = y_i + v_it + 1/2g t^2`
`= 0 + (20.0\ m//s)(5.00\ s) +1/2(-9.80\ m//s^2)(5.00\ s)`
`=-22.5 m`
(A) Using `t_A= 0` as the time the stone leaves the thrower’s hand at position `A`, determine the time at which the stone reaches its maximum height.
Given:
`v_i = 20.0\ m//s`
`g = -9.80\ m//s`
`v_f = 0`
Use Equation: `v_f = v_i + g t`
`=> t = (v_f - v_i)/g`
`=>t=(0-20.0)/9.80 = 20.4 s`
(B) Find the maximum height of the stone.
set `y_i = y_A=0`
`y_f = y_(max) = y_B`
`y_B = y_A +v_it + 1/2 g t^2`
`y_B = 0 + (20.0\ m//s)(2.04\ s) + 1/2(-9.80\ m//s^2)(2.04\ s)^2`
`y_B = 20.4\ m`
(C) Determine the velocity of the stone when it returns to the height from which it was thrown.
Know:`Y_A = Y_C =0`
`v_C^2 = V_A^2 + 2a(Y_C-Y_A)`
Know:`Y_A = Y_C =0`
`=>v_C^2 = V_A^2`
`=> v_C = ±V_A`
since V_C and V_A are opposite,
`=> V_C = - V_A = -20.0\ m//s`
(D) Find the velocity and position of the stone at `t = 5.00\ s`.
`v_D = v_i + g t`
`= 20.0\ m//s + (-9.80\ m//s^2)(5.00\ s)`
`=-29.0\ m//s`
`y_D = y_i + v_it + 1/2g t^2`
`= 0 + (20.0\ m//s)(5.00\ s) +1/2(-9.80\ m//s^2)(5.00\ s)`
`=-22.5 m`