Acceleration
An particle whose velocity is changing is said to be accelerating. For instance, a car whose velocity increases from `0` to `50\ km//h` is accelerating.
The average acceleration `a_(x,avg)` of the particle is defined as the change in velocity `∆v_x` divided by the time interval `∆t` during which that change occurs:
 Average and Instantaneous Acceleration:
Average and Instantaneous Acceleration:
 Example 1:
The velocity of a particle moving along the `x` axis varies according to the expression `v_x = 40 - 5t^2`, where `v_x` is in meters per second and `t` is in seconds.
(A) Find the average acceleration in the time interval `t = 0` to `t = 2.0 s`.
Solution
1. at `t=0` `V_A = 40 - 5(0)^2 = 40 m//s `
2. at `t=2` `V_B = 40 - 5(2)^2 = 20 m//s `
3. `a_avg = (v_B - v_A)/(∆t) = ( 20 - 40)/(2-0) = -10 m//s^2`
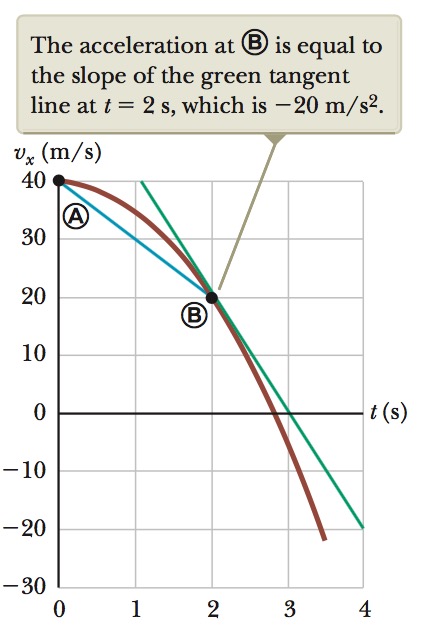
(B) Determine the acceleration at `t = 2.0 s`.
Solution
1. Knowing that the initial velocity at any time `t` is
`v_(x i) = 40 - 5t^2`, find the velocity at any later time `t + ∆t`:
`v_(xf) = 40- 5(t+∆t)^2`
` = 40- 5(t^2 + 2t∆t + (∆t)^2)`
` = 40- 5t^2 - 10t∆t - 5(∆t)^2`
` = v_(x i) - 10t∆t - 5(∆t)^2`
`∆v = v_(xf)-v_(x i) `
` = -10t∆t - 5(∆t)^2`
To find the acceleration at any time t, divide this
expression by `∆t` and take the limit of the result as `∆t` approaches zero:
`a_x = lim_(∆t->0)(∆V_x)/(∆t) = `
`= lim_(∆t->0)(-10t∆t - 5(∆t)^2)/(∆t)`
`= lim_(∆t->0)(-10t - 5∆t)`
`=-10t`
Substitute `t = 2.0 s`:
`a_x = (-10)(2.0) = -20 m//s^2`
Example 1:
The velocity of a particle moving along the `x` axis varies according to the expression `v_x = 40 - 5t^2`, where `v_x` is in meters per second and `t` is in seconds.
(A) Find the average acceleration in the time interval `t = 0` to `t = 2.0 s`.
Solution
1. at `t=0` `V_A = 40 - 5(0)^2 = 40 m//s `
2. at `t=2` `V_B = 40 - 5(2)^2 = 20 m//s `
3. `a_avg = (v_B - v_A)/(∆t) = ( 20 - 40)/(2-0) = -10 m//s^2`
(B) Determine the acceleration at `t = 2.0 s`.
Solution
1. Knowing that the initial velocity at any time `t` is
`v_(x i) = 40 - 5t^2`, find the velocity at any later time `t + ∆t`:
`v_(xf) = 40- 5(t+∆t)^2`
` = 40- 5(t^2 + 2t∆t + (∆t)^2)`
` = 40- 5t^2 - 10t∆t - 5(∆t)^2`
` = v_(x i) - 10t∆t - 5(∆t)^2`
`∆v = v_(xf)-v_(x i) `
` = -10t∆t - 5(∆t)^2`
To find the acceleration at any time t, divide this
expression by `∆t` and take the limit of the result as `∆t` approaches zero:
`a_x = lim_(∆t->0)(∆V_x)/(∆t) = `
`= lim_(∆t->0)(-10t∆t - 5(∆t)^2)/(∆t)`
`= lim_(∆t->0)(-10t - 5∆t)`
`=-10t`
Substitute `t = 2.0 s`:
`a_x = (-10)(2.0) = -20 m//s^2`
`a_(x,avg) = (∆v_x)/(∆t) = (v_(xf) - v_(x i))/(t_f - t_i)`
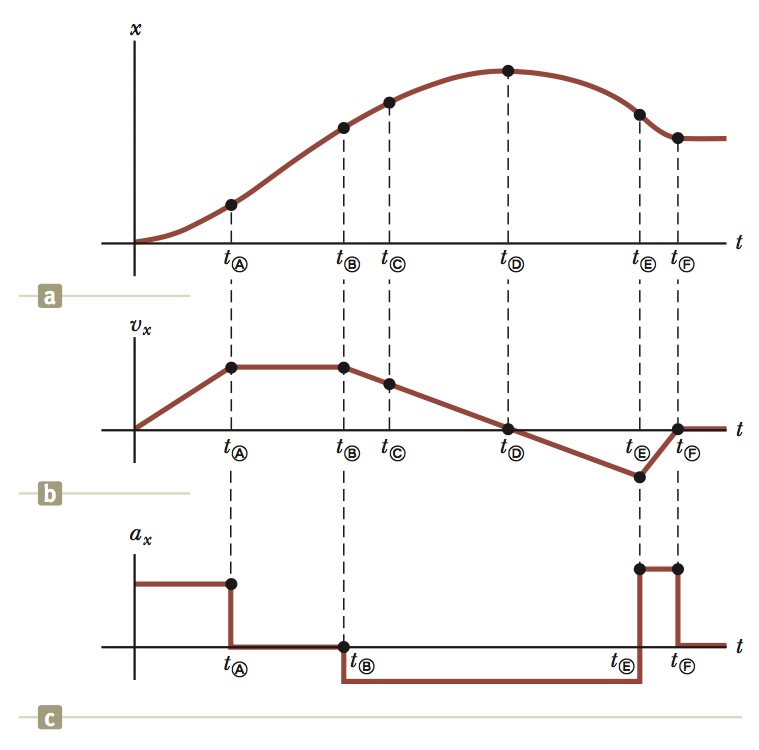
Graphical Relationships Between `x`, `v_x`, and `a_x`
 Average and Instantaneous Acceleration:
Average and Instantaneous Acceleration:
 Example 1:
The velocity of a particle moving along the `x` axis varies according to the expression `v_x = 40 - 5t^2`, where `v_x` is in meters per second and `t` is in seconds.
(A) Find the average acceleration in the time interval `t = 0` to `t = 2.0 s`.
Solution
1. at `t=0` `V_A = 40 - 5(0)^2 = 40 m//s `
2. at `t=2` `V_B = 40 - 5(2)^2 = 20 m//s `
3. `a_avg = (v_B - v_A)/(∆t) = ( 20 - 40)/(2-0) = -10 m//s^2`
(B) Determine the acceleration at `t = 2.0 s`.
Solution
1. Knowing that the initial velocity at any time `t` is
`v_(x i) = 40 - 5t^2`, find the velocity at any later time `t + ∆t`:
`v_(xf) = 40- 5(t+∆t)^2`
` = 40- 5(t^2 + 2t∆t + (∆t)^2)`
` = 40- 5t^2 - 10t∆t - 5(∆t)^2`
` = v_(x i) - 10t∆t - 5(∆t)^2`
`∆v = v_(xf)-v_(x i) `
` = -10t∆t - 5(∆t)^2`
To find the acceleration at any time t, divide this
expression by `∆t` and take the limit of the result as `∆t` approaches zero:
`a_x = lim_(∆t->0)(∆V_x)/(∆t) = `
`= lim_(∆t->0)(-10t∆t - 5(∆t)^2)/(∆t)`
`= lim_(∆t->0)(-10t - 5∆t)`
`=-10t`
Substitute `t = 2.0 s`:
`a_x = (-10)(2.0) = -20 m//s^2`
Example 1:
The velocity of a particle moving along the `x` axis varies according to the expression `v_x = 40 - 5t^2`, where `v_x` is in meters per second and `t` is in seconds.
(A) Find the average acceleration in the time interval `t = 0` to `t = 2.0 s`.
Solution
1. at `t=0` `V_A = 40 - 5(0)^2 = 40 m//s `
2. at `t=2` `V_B = 40 - 5(2)^2 = 20 m//s `
3. `a_avg = (v_B - v_A)/(∆t) = ( 20 - 40)/(2-0) = -10 m//s^2`
(B) Determine the acceleration at `t = 2.0 s`.
Solution
1. Knowing that the initial velocity at any time `t` is
`v_(x i) = 40 - 5t^2`, find the velocity at any later time `t + ∆t`:
`v_(xf) = 40- 5(t+∆t)^2`
` = 40- 5(t^2 + 2t∆t + (∆t)^2)`
` = 40- 5t^2 - 10t∆t - 5(∆t)^2`
` = v_(x i) - 10t∆t - 5(∆t)^2`
`∆v = v_(xf)-v_(x i) `
` = -10t∆t - 5(∆t)^2`
To find the acceleration at any time t, divide this
expression by `∆t` and take the limit of the result as `∆t` approaches zero:
`a_x = lim_(∆t->0)(∆V_x)/(∆t) = `
`= lim_(∆t->0)(-10t∆t - 5(∆t)^2)/(∆t)`
`= lim_(∆t->0)(-10t - 5∆t)`
`=-10t`
Substitute `t = 2.0 s`:
`a_x = (-10)(2.0) = -20 m//s^2`