|
Instantaneous Velocity and Speed (ADVANCED)
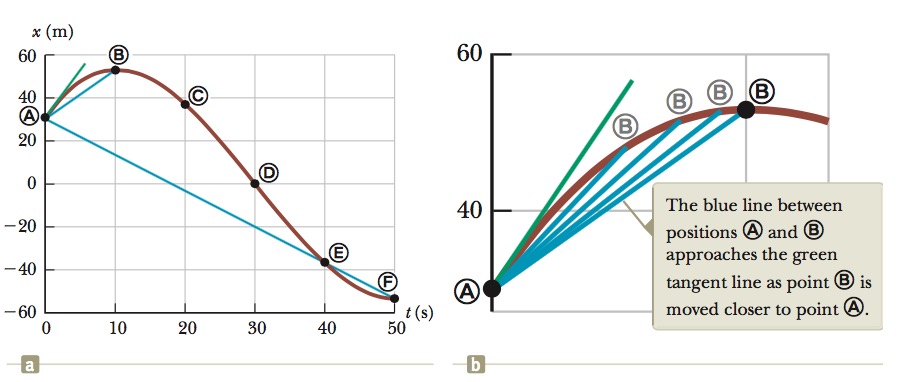
The instantaneous velocity `v_x` equals the limiting value of the ratio `(∆x)/(∆t)` as `∆t` approaches zero:
`v_x = lim_(∆t->0)(∆x)/(∆t)=(dx)/(dt)`
In calculus notation, this limit is called the derivative of `x` with respect to `t`, written `(dx)/(dt)`:
The instantaneous speed of a particle is defined as the magnitude of its instantaneous velocity.
Example:
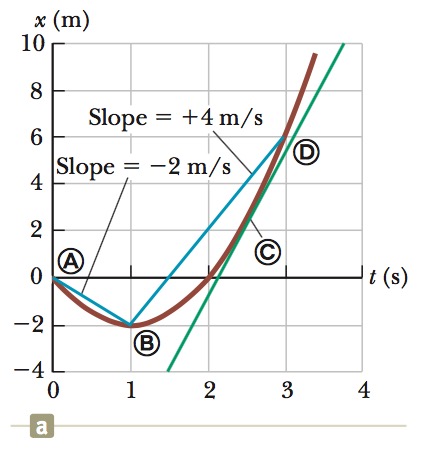
A particle moves along the `x` axis. Its position varies with time according to the expression `x = -4t + 2t^2`, where `x` is in meters and `t` is in seconds. The position–time graph for this motion is shown in above Figure.
(A) Determine the displacement of the particle in the time intervals `t = 0` to `t = 1 s` and `t = 1 s` to `t = 3 s`.
Solution:
Given `x = -4t + 2t^2`
1. in the time intervals `t = 0` to `t = 1 s` (`A->B`)
When `t=0` we get `x_i = -4(0) + 2(0)^2 = 0`
When `t=1` we get `x_f = -4(1) + 2(1)^2 = -2 m`
`∆x_(A->B) = x_f - x_i = -2 - 0 = -2 m`
2. in the time intervals `t = 1` to `t = 3 s`(`B->D`)
When `t=1` we get `x_i = -4(1) + 2(1)^2 = -2 m`
When `t=3` we get `x_f = -4(3) + 2(3)^2 = 6 m`
`∆x_(B->C) = x_f - x_i = 6 - (-2) = 8 m`
(B) Calculate the average velocity during these two time intervals.
Solution:
1. in the time intervals `t = 0` to `t = 1 s` (`A->B`)
`∆t = t_f-t_i = 1-0 = 1s`
`v_(avg)=∆x_(A->B)/∆t = (-2 m) / (1 s) = -2 m//s`
which is same as the slope of line `AB`
2. in the time intervals `t = 1` to `t = 3 s`(`B->D`)
`∆t = t_f-t_i = 3-1 = 2 s`
`v_(avg)=∆x_(B->D)/∆t = (8 m) / (2 s) = 4 m//s`
which is same as the slope of line `BD`
(C) Find the instantaneous velocity of the particle at `t = 2.5 s`.
Solution 1: by measure
The instantaneous velocity at point `C` is the slop of tangent line at point `C`.
In above Figure, the green line is the tangent line at `t = 2.5 s`
Measure the slope of the green line we get
`v_(avg) = (10m - (-4)m)/(3.8s-1.5s) = 6 m//s`
Solution 2: by calculus
Given `x = -4t + 2t^2`
`v_x = (dx)/(dt) = -4 + 2(2)t= -4 +4t`
at `t=2.5s`
`v_x = -4 + (4)(2.5) = 6 m//s`
|
 The instantaneous velocity `v_x` equals the limiting value of the ratio `(∆x)/(∆t)` as `∆t` approaches zero:
`v_x = lim_(∆t->0)(∆x)/(∆t)=(dx)/(dt)`
In calculus notation, this limit is called the derivative of `x` with respect to `t`, written `(dx)/(dt)`:
The instantaneous speed of a particle is defined as the magnitude of its instantaneous velocity.
Example:
The instantaneous velocity `v_x` equals the limiting value of the ratio `(∆x)/(∆t)` as `∆t` approaches zero:
`v_x = lim_(∆t->0)(∆x)/(∆t)=(dx)/(dt)`
In calculus notation, this limit is called the derivative of `x` with respect to `t`, written `(dx)/(dt)`:
The instantaneous speed of a particle is defined as the magnitude of its instantaneous velocity.
Example:
 A particle moves along the `x` axis. Its position varies with time according to the expression `x = -4t + 2t^2`, where `x` is in meters and `t` is in seconds. The position–time graph for this motion is shown in above Figure.
(A) Determine the displacement of the particle in the time intervals `t = 0` to `t = 1 s` and `t = 1 s` to `t = 3 s`.
Solution:
Given `x = -4t + 2t^2`
1. in the time intervals `t = 0` to `t = 1 s` (`A->B`)
When `t=0` we get `x_i = -4(0) + 2(0)^2 = 0`
When `t=1` we get `x_f = -4(1) + 2(1)^2 = -2 m`
`∆x_(A->B) = x_f - x_i = -2 - 0 = -2 m`
2. in the time intervals `t = 1` to `t = 3 s`(`B->D`)
When `t=1` we get `x_i = -4(1) + 2(1)^2 = -2 m`
When `t=3` we get `x_f = -4(3) + 2(3)^2 = 6 m`
`∆x_(B->C) = x_f - x_i = 6 - (-2) = 8 m`
(B) Calculate the average velocity during these two time intervals.
Solution:
1. in the time intervals `t = 0` to `t = 1 s` (`A->B`)
`∆t = t_f-t_i = 1-0 = 1s`
`v_(avg)=∆x_(A->B)/∆t = (-2 m) / (1 s) = -2 m//s`
which is same as the slope of line `AB`
2. in the time intervals `t = 1` to `t = 3 s`(`B->D`)
`∆t = t_f-t_i = 3-1 = 2 s`
`v_(avg)=∆x_(B->D)/∆t = (8 m) / (2 s) = 4 m//s`
which is same as the slope of line `BD`
(C) Find the instantaneous velocity of the particle at `t = 2.5 s`.
Solution 1: by measure
The instantaneous velocity at point `C` is the slop of tangent line at point `C`.
In above Figure, the green line is the tangent line at `t = 2.5 s`
Measure the slope of the green line we get
`v_(avg) = (10m - (-4)m)/(3.8s-1.5s) = 6 m//s`
Solution 2: by calculus
Given `x = -4t + 2t^2`
`v_x = (dx)/(dt) = -4 + 2(2)t= -4 +4t`
at `t=2.5s`
`v_x = -4 + (4)(2.5) = 6 m//s`
A particle moves along the `x` axis. Its position varies with time according to the expression `x = -4t + 2t^2`, where `x` is in meters and `t` is in seconds. The position–time graph for this motion is shown in above Figure.
(A) Determine the displacement of the particle in the time intervals `t = 0` to `t = 1 s` and `t = 1 s` to `t = 3 s`.
Solution:
Given `x = -4t + 2t^2`
1. in the time intervals `t = 0` to `t = 1 s` (`A->B`)
When `t=0` we get `x_i = -4(0) + 2(0)^2 = 0`
When `t=1` we get `x_f = -4(1) + 2(1)^2 = -2 m`
`∆x_(A->B) = x_f - x_i = -2 - 0 = -2 m`
2. in the time intervals `t = 1` to `t = 3 s`(`B->D`)
When `t=1` we get `x_i = -4(1) + 2(1)^2 = -2 m`
When `t=3` we get `x_f = -4(3) + 2(3)^2 = 6 m`
`∆x_(B->C) = x_f - x_i = 6 - (-2) = 8 m`
(B) Calculate the average velocity during these two time intervals.
Solution:
1. in the time intervals `t = 0` to `t = 1 s` (`A->B`)
`∆t = t_f-t_i = 1-0 = 1s`
`v_(avg)=∆x_(A->B)/∆t = (-2 m) / (1 s) = -2 m//s`
which is same as the slope of line `AB`
2. in the time intervals `t = 1` to `t = 3 s`(`B->D`)
`∆t = t_f-t_i = 3-1 = 2 s`
`v_(avg)=∆x_(B->D)/∆t = (8 m) / (2 s) = 4 m//s`
which is same as the slope of line `BD`
(C) Find the instantaneous velocity of the particle at `t = 2.5 s`.
Solution 1: by measure
The instantaneous velocity at point `C` is the slop of tangent line at point `C`.
In above Figure, the green line is the tangent line at `t = 2.5 s`
Measure the slope of the green line we get
`v_(avg) = (10m - (-4)m)/(3.8s-1.5s) = 6 m//s`
Solution 2: by calculus
Given `x = -4t + 2t^2`
`v_x = (dx)/(dt) = -4 + 2(2)t= -4 +4t`
at `t=2.5s`
`v_x = -4 + (4)(2.5) = 6 m//s`